
拋硬幣的最早記載可追溯至羅馬時期,當時人們認為拋出正面或反面的機率為神性意志的展現。雖然直至今日已經沒有那麼嚴肅,但拋硬幣仍被認為是做決定或解決爭端的公平方式。在某些體育賽事中,拋硬幣用於決定隊伍的進攻方向,或者在平局時選出獲勝者。但拋硬幣究竟有多隨機呢?曾為職業魔術師的佩爾西‧戴康尼斯(Persi Diaconis)後來成為了史丹佛大學的數學和統計學家,他對這個問題的答案很感興趣。
2007年,戴康尼斯和來自史丹佛與加利福尼亞大學聖克魯茲分校的研究夥伴們進行了實驗,包括拋擲一枚繫著絲帶的硬幣,藉由解開硬幣上的絲帶來確定硬幣旋轉的次數。為了消除拋硬幣過程中不希望出現的人為變數,拋硬幣的初始條件必須一致,因此他們委託哈佛大學製作拋硬幣機來進行實驗。此外,他們還使用高速攝像機捕捉每次拋硬幣的慢動作照片,以精確的角度測量硬幣的翻轉方向。
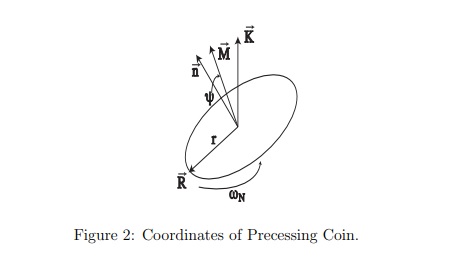
結果發現,當初始條件完全相同時,拋硬幣能產生相同的結果,這意味著拋硬幣的隨機性很可能是由於每個人的拋擲方式不同(拋擲的速度和高度、接硬幣時的角度和翻轉程度等等)所造成。儘管用手拋硬幣看似具有不可預測性,但仍然存在固有的偏差:如果硬幣一開始是正面,那麼最後有51%的可能性硬幣會落在同一面,而不是反面。也就是說,原本應該是一半一半的機率產生了偏差,變成了51%對49%。
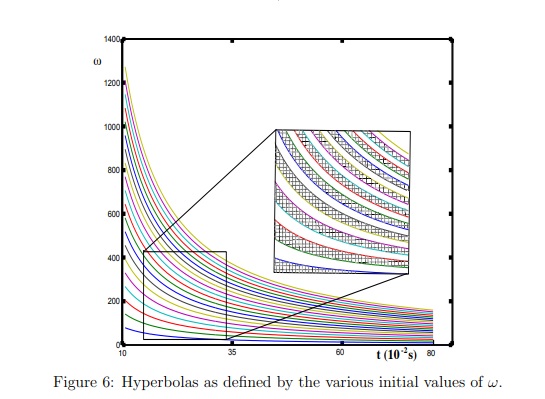
偏差的幅度取決於一件事:硬幣的垂直向量與角動量向量之間的「角度A」(在拋硬幣的過程中都不會改變)。他們觀察真人大量硬幣的結果,並借助高速攝像機測量角度A的分佈,證明了拋硬幣的偏差至少為1%。如果加以運用這種偏差,魔術師和賭徒是有能力操控拋硬幣的結果。因此在足球比賽開球拋硬幣選邊時,硬幣不得用手接住,而是讓硬幣自然落至地面。
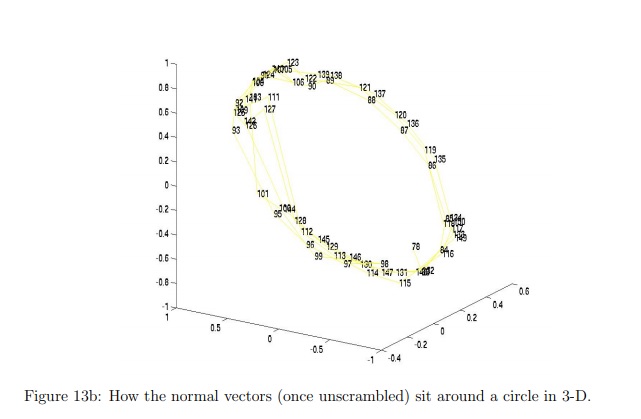
這項研究得出的結論是,經典的拋硬幣假設依然成立,即拋硬幣結果為正面或反面的統計學機率為二分之一。因此,為了提高拋硬幣的公平性,應該盡可能讓初始條件變得隨機,例如讓硬幣從口袋裡拋出來,或是在拋硬幣前用雙手蓋住搖晃才拋擲。此外,不是拋硬幣的人應該在硬幣還在空中時就選擇正面或反面,如此一來拋硬幣的人就不能用朝對自己有利的方式拋擲。
研究全文:
〈Dynamical Bias in the Coin Toss〉─Persi Diaconis, Susan Holmes and Richard Montgomery,《Society for Industrial and Applied Mathematics》,2007。









 最新文章
最新文章 主題總覽
主題總覽 成為粉絲
成為粉絲 在IG上追蹤
在IG上追蹤 RSS訂閱
RSS訂閱 合作提案
合作提案 贊助我們
贊助我們